
Cross Layer Transcoders for the Qwen3 LLM Family
Digging Into Interpretable Features
This post was originally published on Less Wrong
Sparse autoencoders SAEs and cross layer transcoders CLTs have recently been used to decode the activation vectors in large language models into more interpretable features. Analyses have been performed by Goodfire, Anthropic, DeepMind, and OpenAI.
BluelightAI has constructed CLT features for the Qwen3 family, specifically Qwen3-0.6B Base and Qwen3-1.7B Base, which are made available for exploration and discovery here. In addition to the construction of the features themselves, we enable the use of topological data analysis (TDA) methods for improved interaction and analysis of the constructed features.

Signal Processing for AI
Solving Model Errors at the Source
Signal processing consists of the extraction of information usable by a mathematical model from raw data. It is a critical element in many engineering domains, including imaging, audio, speech, radar, and many others. It includes filtering tasks to remove noise, say in images or audio, Fourier transform techniques for audio, as well as more complex tasks such as location and reconstruction of objects using radar or sonar.
Graph Modeling for Mechanistic Interpretability
Turning Complex AI Models into Searchable Graphs
The problem of extracting human-understandable information from large, complex, and noisy text or image data is one of the fundamental challenges facing artificial intelligence. Modern AI models (esp. LLMs) can deliver amazing outputs, but their decision-making processes often remain hidden, creating a “black box” that makes it difficult to know why models fail or succeed.
BluelightAI’s flagship interpretability platform, Cobalt, directly addresses this AI black box problem by leveraging Topological Data Analysis (“TDA”) as a foundational technology, a critical differentiator unmatched by existing evaluation platforms. The fundamental idea behind TDA is that for many kinds of data, traditional algebraic tools are not flexible enough to represent data as effectively as we would like.

Topological Feature Generation for Speech Recognition
How smart feature engineering improves speech recognition
In our earlier blog we showed that topological techniques can be used to improve the performance of convolutional neural networks being used for image classification. Specifically, we used features parametrized by a geometric object called a Klein bottle as well as an architecture guided by the same object to drastically speed up the learning rate, but more importantly to improve generalization. We believe that generalization is a good measure of progress toward Artificial General Intelligence.

Feature Engineering for Language Models
Using parts of speech to improve language model performance
V. Lado Naess, L. Sjögren, D. Fooshee, G. Carlsson
In our earlier post “Improving CNNs with Klein Networks: A Topological Approach to AI,” we observed that adding predefined interpretable features to a CNN, and even modifying its architecture, resulted in significant improvement in its performance. Speed of learning was of course greatly improved, but it turned out that generalization was also greatly improved. Moreover, the insights thus obtained allowed us to construct new features for video that greatly improved performance on a video classification task. These observations led us to ask if the addition of predefined interpretable features to Large Language Models could also lead to improvements in their performance. In this post we report findings from experiments we performed on a language model by adjoining features constructed from parts of speech tagging applied to the input data.

Mechanistic Interpretability in Practice: Applying TDA to Breast Cancer
This paper, which we shared last week, is a demonstration of how topological data analysis methods can be used for feature engineering and selection for data sets where there are many features, or columns in the data matrix.
In our Less Wrong post we pointed out that when a data set is “wide”, i.e. includes a large number of features, it is useful to compress the feature set into a graph structure where each node corresponds to a set of features. This gives an overview of what otherwise might be a feature set which is very hard to understand. Each data point can also be treated as a function on the nodes of the corresponding graph, so that one can examine and compare data points or collections of data points by “graph heat maps”, i.e. colorings of the nodes representing the functional values.
Mechanistic interpretability serves as the unifying macro concept here, as both sources leverage feature compression and graph-based visualization to transform high dimensional, opaque systems into interpretable structures that reveal underlying relationships. This paper studies a particular wide data set, where the features correspond to genes, with the entries being gene expression levels.
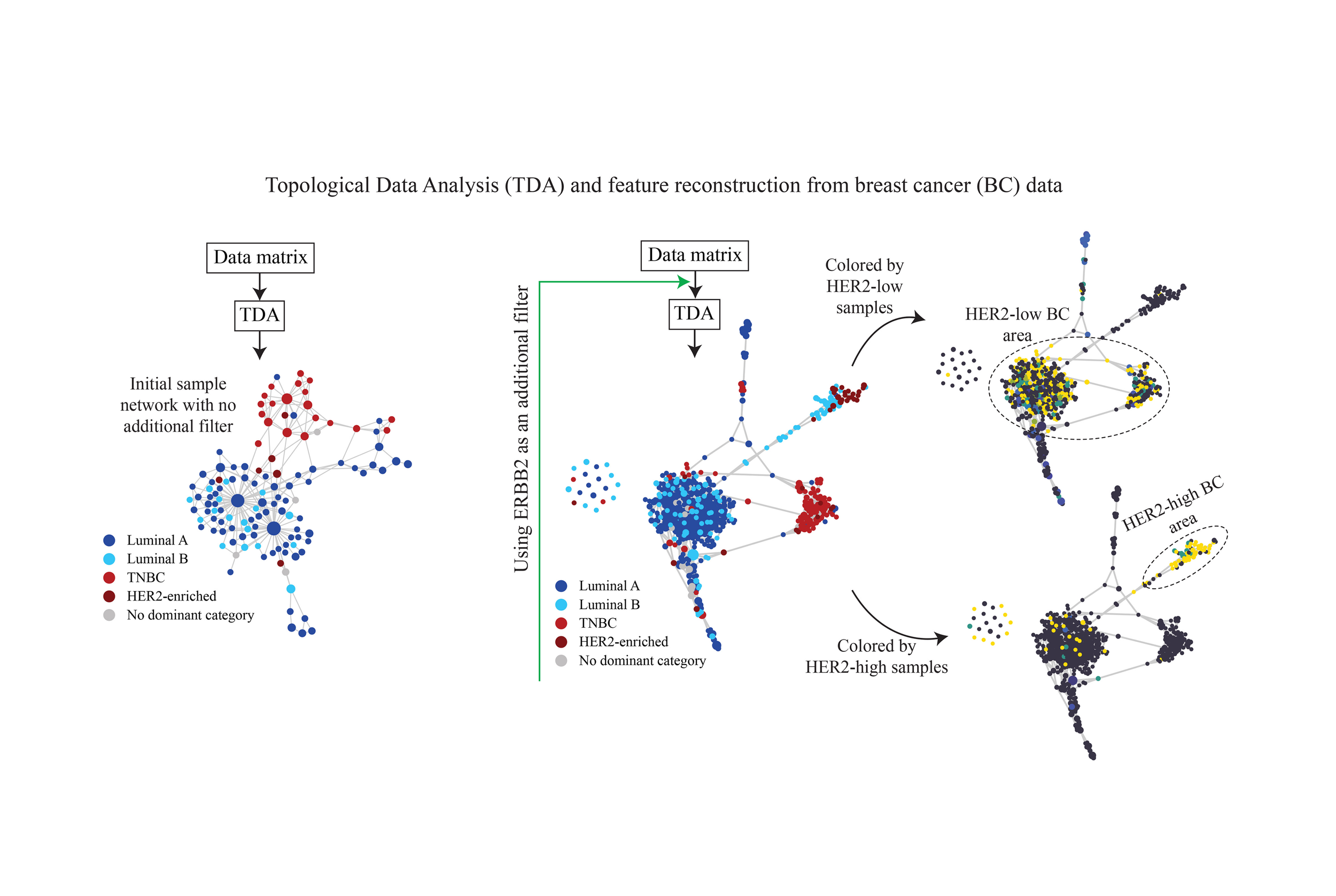
Topological Data Analysis Reveals a Subgroup of Luminal B Breast Cancer
This paper was originally published in the IEEE Open Journal of Engineering in Medicine and Biology.
Impact Statement:
High dimensional data is difficult to visualize or analyze. Reducing the dimension of data while preserving its veracity has become a key challenge for data science. A key tenet of data is its shape that can be topologically defined. In this study, we use the shape or topology of data to infer features that potentially carry valuable information. We use BC data as an example owing to its importance and complexity. The heterogeneity of BC data makes interpretation and prognosis difficult. We show that topological analysis of BC data and its graphical representation provide a natural subtyping in addition to parsing the associated features. Interestingly, the topological analysis points to a novel HER-2 positive luminal subtype, suggesting alternate therapeutic interventions.

Next Generation AI Model Evaluation
Go beyond the leaderboard: How TDA uncovers what benchmark scores miss in model evaluation.
The evaluation of models is absolutely critical to the artificial intelligence enterprise. Without an array of evaluation methods, we will not be able to understand whether the models are doing what we want them to do, or what measures we should take to improve them. Another reason for the need for good evaluation measures is that once an AI model is deployed, we will find that the input data, the interaction of users with the model, and the user reactions to the output of the model will change over time. This means that not only do we need evaluation at the time of construction of the model, we will need to evaluate continually throughout the deployment lifecycle of the model.

Improving CNNs with Klein Networks: A Topological Approach to AI
This article was originally published in LessWrong.
In our earlier post, we described how one could parametrize local image patches in natural images by a surface called a Klein bottle. In Love et al, we used this information to modify the convolutional neural network construction so as to incorporate information about the pixels in a small neighborhood of a given pixel in a systematic way. We found that we were able to improve performance in various ways. One obvious way is that the neural networks learned more quickly, and we therefore believe that they could learn on less data. Another very important point, though, was that the new networks were also able to generalize better. We carried out a synthetic experiment on MNIST, in which we introduced noise into MNIST. We then performed two experiments, one in which we trained on the original MNIST and evaluated the convolutional models on the “noisy” set, and another in which we trained on the noisy set and evaluated on the original set. The results are displayed below.

From Loops to Klein Bottles: Uncovering Hidden Topology in High Dimensional Data
Motivation: Dimensionality reduction is vital to the analysis of high dimensional data. It allows for better understanding of the data, so that one can formulate useful analyses. Dimensionality reduction that produces a set of points in a vector space of dimension n, where n s much smaller than the number of features N in the data set. If the number n is 1, 2, or 3, it is possible to visualize the data and obtain insights. If n is larger, then it is more difficult. One interesting situation, though, is where the data concentrates around a non-linear surface whose dimension is 1, 2, or 3, but can only be embedded in a dimension higher than 3. We will discuss such examples in this post.

Geometry of Features in Mechanistic Interpretability
This post is motivated by the observation in Open Problems in Mechanistic Interpretability by Sharkey, Chugtai, et al that “SDL (sparse dictionary learning) leaves feature geometry unexplained”, and that it is desirable to utilize geometric structures to gain interpretability for sparse autoencoder features.
We strongly agree, and the goal of this post is to describe one method for imposing such structures on data sets in general. Of course, it applies particularly to the case of sparse autoencoder features in LLM’s. The need for geometric structures on feature sets applies generally in the data science of wide data sets (those with many columns), such as occur as the activation data sets in complex neural networks. We will give some examples in the life sciences, and conclude with one derived from LLM’s.

Topological Data Analysis and Mechanistic Interpretability
In this post, we’ll look at some ways to use topological data analysis (TDA) for mechanistic interpretability.
We’ll first show how one can apply TDA in a very simple way to the internals of convolutional neural networks to obtain information about the “responsibilities” of the various layers, as well as about the training process. For LLM’s, though, simply approaching weights or activations “raw” yields limited insights, and one needs additional methods like sparse autoencoders (SAEs) to obtain useful information about the internals. We will discuss this methodology, and give a few initial examples where TDA helps reveal structure in SAE feature geometry.
