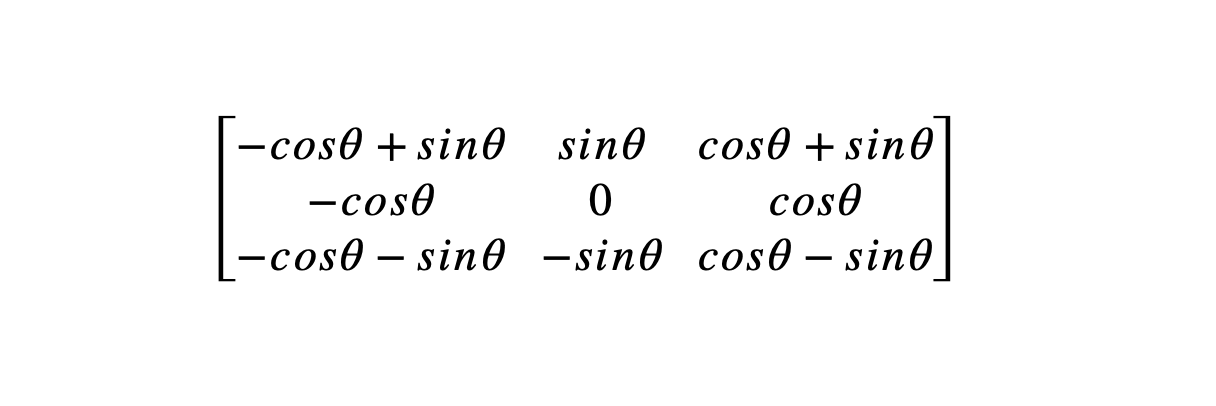Topological Feature Generation for Speech Recognition
How smart feature engineering improves speech recognition
In our earlier blog we showed that topological techniques can be used to improve the performance of convolutional neural networks being used for image classification. Specifically, we used features parametrized by a geometric object called a Klein bottle as well as an architecture guided by the same object to drastically speed up the learning rate, but more importantly to improve generalization. We believe that generalization is a good measure of progress toward Artificial General Intelligence.
In two papers (see here and here), Zhiwang Yu et al have applied the same ideas for predicting and classification phonemes in speech. Roughly speaking, the ideas consist of two steps. The first step is to recognize that speech recognition can be viewed as an image recognition problem via a transformation which assigns to a raw speech waveform a spectrogram, which can be viewed as an image. The second step is to recognize that the spectrogram is actually a very special kind of image, and that therefore new features can be created which perform better than generic image features. We’ll give a brief summary of these constructions.
Spectrograms are constructed from the Fourier transform of the raw audio signal. Since the signal is time dependent, one can consider a color coded plot in the plane, where the plane coordinates are frequency f and the time t. The value at a particular point (f,t) is the frequency of the signal at that time point. Here is a typical spectrogram, specifically a Mel spectrogram.
As you can see, it looks nothing like a natural image. However, we can try standard convolutional networks or the Klein boosted networks for classification. In this case, the classification problem, rather than being for hand drawn digits, consists of phonemes. Phonemes are short sequences of audio, that are identified by two letter codes. Here is a table that shows you what is being classified, from the ARPABET-IPA phonetic notation. Each audio sample will have a 2 letter code attached, and that is what is being classified in Yu et al.
In order to describe the approach taken in Yu et al, let’s first recall how the Klein bottle elements can be interpreted as matrices. An edge detector for an edge at an angle an be described as forming a dot product with the array
The line detectors in the Klein bottle can similarly be described with a more complex array depending on. The features given in Yu et al are described as dot products with other arrays. The key point of these features is that they choose not to enforce rotational invariance, since the role of the two directions (time and frequency) are quite distinct and rotational invariance is not to be expected. Instead, they use the intuition that the arrays should incorporate the features that are useful in one-dimensional convolutional neural networks for time series in the time direction. The arrays they choose are of the form
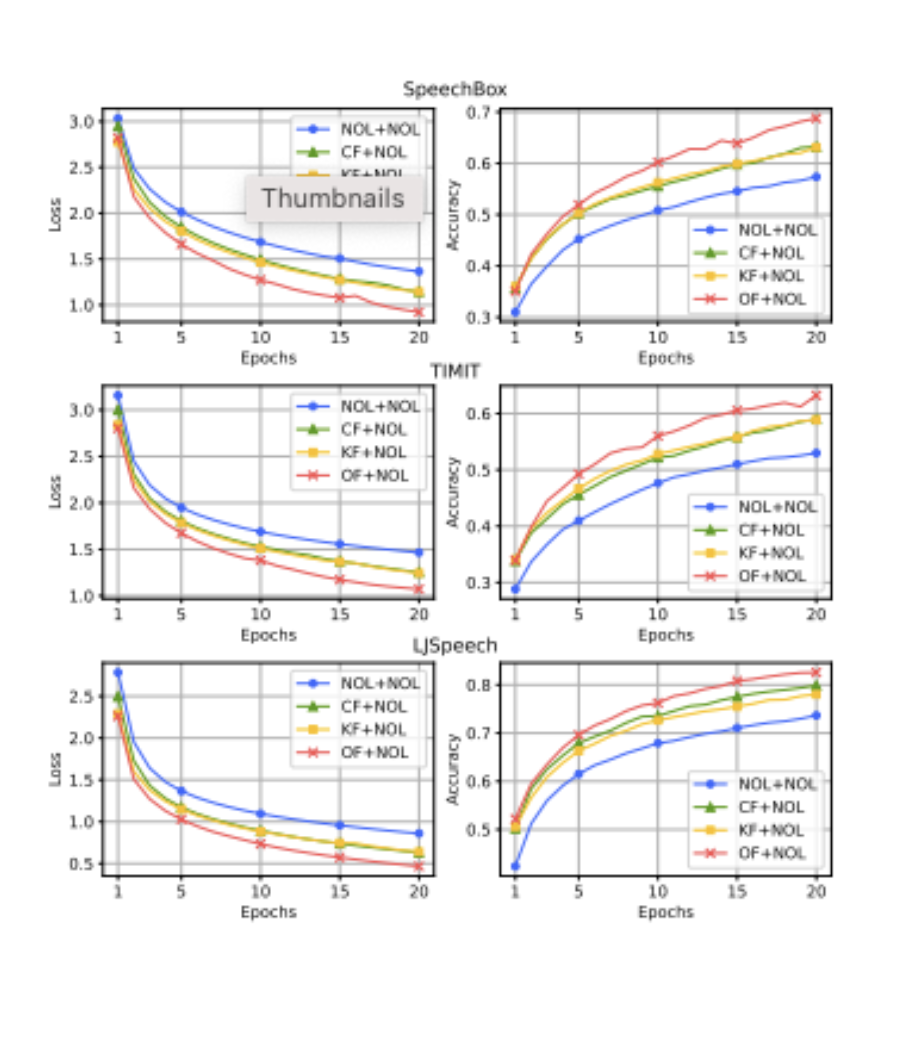
where is a general orthogonal matrix. The two reflect the injection of the discrete approximations of the first and second derivatives in time series analysis. Here are a couple of samples of the results they obtained. The first figure shows the performance on three separate data sets, called SpeechBox, TIMIT, and LJSpeech, showing accuracy and loss vs. number of training epochs. There are curves for ordinary convolutional neural networks (NOL + NOL, blue curve), two versions of the Klein boosted neural networks (CF + NOL and KF + NOL, green and yellow curves respectively), and the neural networks based on the specialized constructions made in this paper (OF + NOL, pink curve) . In all cases, OF + NOL performs best validating the papers hypothesis that features specialized for spectrograms should perform better than general purpose image classifiers.
In a second analysis, Yu et al considered performance on SpeechBox under various signal to noise conditions. The results look like this.
As you can see, for SNR = 20, the results mirror the earlier results. In the case of SNR = 0, though, one of the Klein models outperformed the OF + NOL model. This is the more complex of the Klein models, one including the “secondary circles” which detect lines. In other words, the Klein model performed better in very noisy situations. It would be very interesting to explore why this is, and to ask whether the OF + NOL model can be augmented in a systematic way to improve its performance on noisy audio data.
We found this paper very interesting, and believe that it provides further evidence that smart feature generation and engineering can improve the performance of neural networks.